A couple of posts in this blog started with a game mechanic, explored a problem behind it, and offered a solution (hopefully, an interesting one). For example, we looked at a variation of depth-first search in a Cyberpunk 2077 minigame and dynamic programming in FTL: Faster Than Light. In this post, we’ll do something similar. We’ll have a look at Triple Triad, a card minigame from Final Fantasy VIII, see how we can approach its board logic, and implement it using ARM’s NEON intrinsics.

Released back in 1999, Final Fantasy VIII remains a somewhat divisive entry in the series. Still it gets a lot of praise for its epic soundtrack, great graphics (by the 1999 standards, that is), and, of course, Triple Triad, the addictive card minigame that became a fan favorite. I’ve lost count of how many times I’ve beaten the game, but in every single playthrough, I ended up spending a lot of time just playing cards with various NPCs. At this point, I’ve started to think of Final Fantasy VIII as a series of events that keep distracting me from playing Triple Triad.

Anyhow, if you’re not familiar with this 1999 gem and its card game, the rules are quite simple. There are two players in the game. Each of them has five cards, marked by one color:

The cards have four values: top, right, bottom, and left — ranged from 1 to A (A being a moniker for 10). Each player, in their turn, places a card on a 3x3 board. If a newly placed card happens to have neighbors on either axis, the game checks their adjacent values: the card’s top value against the neighbor’s bottom one, the card’s right against the neighbor’s left, and so on. If any of the new card’s values is greater than the adjacent values, the neighbor card flips and goes to the player:

These simple rules are getting extended and more complicated as the game progresses and the player visits various regions in the game. The basics, however, stay the same, and that’s what we’re going to focus on.

Playing Final Fantasy VIII, or, rather, Triple Triad, I’ve always wondered: how would I implement the game, specifically its board logic? Which eventually made me open a code editor and start to actually implement it. A huge disclaimer before we go further: I’m by no means an expert in programming games and have little to no idea how they actually work under the hood¹. The following is just a programming exercise for funsies, please don’t try it in your games.

First Pass

The simplest idea for the board logic implementation would probably be straightforward. Create the board as a 3x3 matrix, introduce cards, and compare their adjacent values. So, let’s start with this setup and see what it would look like.

Since the board would need to reference cards, we’ll start with defining a card first. And right off the bat we introduce a card with a few somewhat unexpected specifics:

public struct Card(short owner, short top, short right, short bottom, short left)
{
  public short Owner = owner;
  public readonly short Top = top;
  public readonly short Right = right;
  public readonly short Bottom = bottom;
  public readonly short Left = left;
}

First, we make it a struct. Not only because it only holds a few value types, but this will also help us simplify the board logic by removing null checks and initialization.

Second, we add Owner as short, which might be surprising. Common practice would probably be to introduce an enum with defined values, like None if the card is available, Player for the player, and AI for the AI opponent. Instead, we’ll treat 0 as available, 1 for the player, and 2 — AI, we’ll go back to why we chose short a bit later.

Finally, we’ll use short for the card values too, which again may be unusual. We only have 10 possible values, so why not go at least with byte, the smallest possible value on which we can perform operations? Again, we’ll come to the reason a bit later.

Now that we have the cards, we can create the board:

public class Board
{
  private readonly Card[,] _cards = new Card[3, 3];
}

Which, as described earlier, is just a 3x3 matrix. Since we have implemented cards as a two-dimensional array of structs, we don’t need to initialize it. Every card by default has Owner and all values set to 0. The board would probably need only two methods, Add and GetAll. The former would add a card to the board and do the heavy-lifting: compare the card values and flip neighbor cards. Meanwhile, the latter would return the cards, so that the client can render the board.

For brevity, let’s assume that we’ve verified the input already, so we shouldn’t need to worry about edge cases, such as placing a card in a slot that had already been taken. Let’s start with Add as it’s a more complicated method:

public void Add(int row, int col, Card card)
{
  _cards[row, col] = card; // (1)

  if (row > 0) // (2)
  {
    ref var topNeighbor = ref _cards[row - 1, col]; // (3)
    if (CanFlip(card, topNeighbor) && topNeighbor.Bottom < card.Top) // (4)
    {
      topNeighbor.Owner = card.Owner; // (5)
    }
  }
  if (col < _cards.GetLength(1) - 1)
  {
    ref var rightNeighbor = ref _cards[row, col + 1];
    if (CanFlip(card, rightNeighbor) && rightNeighbor.Left < card.Right)
    {
      rightNeighbor.Owner = card.Owner;
    }
  }
  if (row < _cards.GetLength(0) - 1)
  {
    ref var bottomNeighbor = ref _cards[row + 1, col];
    if (CanFlip(card, bottomNeighbor) && bottomNeighbor.Top < card.Bottom)
    {
      bottomNeighbor.Owner = card.Owner;
    }
  }
  if (col > 0)
  {
    ref var leftNeighbor = ref _cards[row, col - 1];
    if (CanFlip(card, leftNeighbor) && leftNeighbor.Right < card.Left)
    {
      leftNeighbor.Owner = card.Owner;
    }
  }
}

It probably looks quite straightforward already, but let’s go over it and see how it works in detail anyway:

1. We place a card in a specified slot indexed by row and col. Since we’re working with a two-dimensional array, the indexing is not working as X and Y on a 2D plane, rather the other way around: first rows, then columns.
2. Then we see if the card has a top neighbor. Cards in row 0 don’t have them, so we have to be careful.
3. If the neighbor is there, we do something a bit tricky. We can just refer to the top neighbor as _cards[row - 1, col], but this looks somewhat clunky, so we name it as topNeighbor. However, later we might want to modify its Owner, and we can’t do that without ref because the card is a struct, so we’d be modifying a copy of _cards[row - 1, col]. Hence, we mark it with ref.
4. We check if we can flip a card with CanFlip, that is, if the neighbor has a non-zero Owner, which should be different from our card’s Owner.
5. And if it’s the case, we change the owner.

Method CanFlip mentioned in 4 looks simple enough to leave it without an explanation:

private static bool CanFlip(Card card, Card other)
{
  if (other.Owner == 0) return false;
  return card.Owner != other.Owner;
}

Then we apply the same steps to other three neighbors one by one.

Once we have placed the card and flipped the neighbors, we should provide a method to the caller for checking the current state of the board, GetAll:

public ReadOnlySpan<Card> GetAll()
{
  return MemoryMarshal.CreateReadOnlySpan(ref _cards[0, 0], _cards.Length);
}

We do that by using a handy MemoryMarshal.CreateReadOnlySpan method, which takes a reference to a managed object and its length and creates a read-only span over it.

While this implementation is quite straighforward, I’m not sure I like all this branching when handling neighbors. Besides, we need to do the same operation four times. So, what if we could remove the branching entirely and even do all value comparisons at the same time?

Branchless Approach

So far our board looks like this:

You know where the branching stems of in the implementation above? Handling corner cases. Edge slots on all four sides of the board don’t have neighbors, and we have to take that into account. But what if we extend the board so that each slot always has four neighbors? We can do that by adding 12 more additional slots. At the same time, we’ll also switch indexing from rows and columns to just integers from 0 to 20. So our board now looks like this:

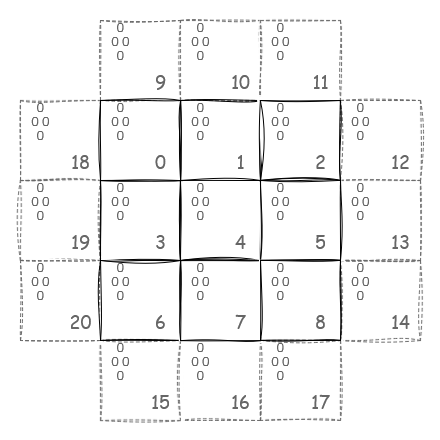
Now we see that whenever we select a game slot from 0 to 8, we always get four neighbors and process them at once.

Let’s take a look at an example to see how it works in practice. Say, we have played three turns already and the board looks like this:

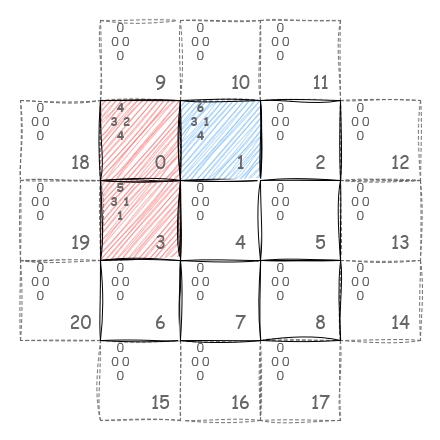
First, the AI (playing for the reds) places its card at 0. Then the player places their card at 1, flipping AI’s card at 0. Finally, the AI places a new card at 3, getting its first card back. Now the player wants to place a card at 4:

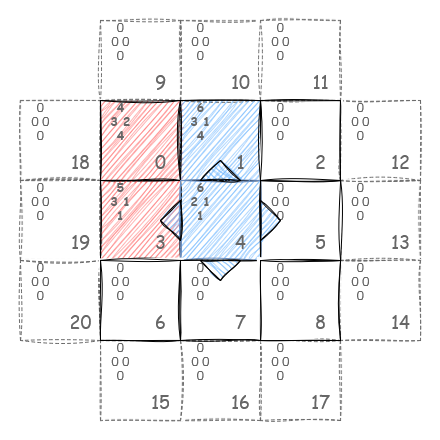
In order to process the turn, we need to perform two things: compare the values and figure which neighbors we should flip.

To compare the values, we need to create two arrays: one with the values of the card we are about to place on the board, and the other with adjacent values of the neighbor cards, then compare arrays’ elements:

card     = [6, 1, 1, 2]
adjacent = [4, 0, 0, 1]
result   = [true, true, true, true]

To know which element corresponds to card values, let’s borrow an idea from (sigh) CSS and go in the clockwise direction: top, right, bottom, left. The elements in result indicate that all card values are greater than the corresponding values in adjacent.

Next, we need to check which neighbors to flip. It’s a bit tricky as we don’t want to flip an empty card with Owner equal to 0 as it represents an available slot. So we split the flip operation into a few steps.

First, we create a new array owners, which has Owner values from neighbor cards and we again go in the clockwise direction, starting from the top:

owners = [1, 0, 0, 2]

Then we check if neighbor cards currently belong to anyone. We can do that by comparing array elements against elements of a zero array. Since 0 represents no owner, we will get a result consisting of either false for the empty neighbor, or true for a neighbor that has an owner:

owners    = [1, 0, 0, 2]
zeroes    = [0, 0, 0, 0]
neighbors = [true, false, false, true]

Next, based on this information we have to decide which neighbor to flip by applying the logical AND operation to the comparison result, result, and the neighbors array. Which would result in another array select. An item with false would indicate that the neighbor card is weaker or it’s empty, thus we don’t flip it. An item with true indicates that the card is stronger and the neighbor belongs to the opponent, thus it should be flipped. It’s worth noting that the card might already belong to the current player, not the opponent, so changing the owner would actually do nothing.

result    = [true, true, true, true]
neighbors = [true, false, false, true]
select    = [true, false, false, true]

Finally, we need to do the actual flipping of each neighbor. If an item in select is true, we flip the neighbor, setting the player as its Owner. If the item is false, we do nothing, keeping the original owner.

Once we performed all steps, we should get the result on the board:

Now let’s get back to the code and see how we can implement this algorithm.

SIMD Implementation

There are several ways to implement the idea described above. However, we’ve already discussed packing various data, card values and owners, into arrays and doing operations on all elements at once. From this, it should be pretty clear that we can use an old favorite — SIMD, which stands for “single instruction, multiple data”.

Alternatively, since we are dealing with relatively small numbers (card values only need 10 values, owners take only 3), we can pack them into scalar numbers, like 32-bit integers, and do some bit magic to manipulate them. Unlike SIMD, it would even benefit from being platform-independent. However, we are here for fun and learning, so why not explore something new? Something we have not taken a look at in this blog yet, ARM NEON instrinsics.

NEON intrinsics are functions available in some languages that map directly to NEON SIMD instructions. They’re somewhat similar to x64 intrinsics, with which we have worked before, but provide smaller registers in size (at least at the time of writing) and, of course, a different set of intrinsics.

Luckily for us, .NET does provide access to NEON intrinsics starting from .NET 5, so we can use them directly. In addition to that, its API might also look familiar as it mirrors the API of the x64 intrinsics:

if (AdvSimd.IsSupported)
{
  var vector1 = Vector128.Create(1, 2, 3, 4);
  var vector2 = Vector128.Create(6, 7, 8, 9);
  var result = AdvSimd.Add(vector1, vector2); // => <7, 9, 11, 12>
}

I’m writing this post on an Apple computer equipped with an M-series chip, which is based on the ARM architecture, so I’ll skip this check in the implementation for brevity (and keeping the implementation truly branch-free).

So, coming back to our problem, we only have four small elements to pack. The smallest vector that’s available for us is a 64-bit vector. If we were to represent card values and owners as bytes, we would have needed to pad the vector with 0s:

var vector = Vector64.Create(card.Top, card.Right, card.Bottom, card.Left, 0, 0, 0, 0);

And always remember to ignore the padding. Foreshadowing this decision, we decided to go with shorts which take 16 bits — way more than we need — but the vector would look nicer:

var vector = Vector64.Create(card.Top, card.Right, card.Bottom, card.Left);

Before diving into vectors, though, we have to complete the initial setup described above. First thing we need is to create a new board:

public class SimdBoard
{
  private readonly Card[] _cards = new Card[9 + 12];
}

Now we just need a one-dementional linear array of 9 cards and the additional 12 for virtual neighbors of the edges cards. The new indexing approach, however, introduces a challenge — now we need to know what neighbors each card has. So, somewhere in code we have to have this lookup table:

private readonly Dictionary<(int, int), int[]> _neighbors = new()
{
  {(0, 0), [09, 01, 03, 18]},
  {(0, 1), [10, 02, 04, 00]},
  {(0, 2), [11, 12, 05, 01]},
  {(1, 0), [00, 04, 06, 19]},
  {(1, 1), [01, 05, 07, 03]},
  {(1, 2), [02, 13, 08, 04]},
  {(2, 0), [03, 07, 15, 20]},
  {(2, 1), [04, 08, 16, 06]},
  {(2, 2), [05, 14, 17, 07]},
};

To keep the same signature for the Add method we’ll still take row and col for the card position, but then immediately map it onto the array of neighbors. Finally, the most interesting part of this implementation — the Add method itself:

public void Add(int row, int col, Card card)
{
  _cards[3 * row + col] = card; // (1)
  var n = _neighbors[(row, col)]; // (2)

  var owners = Vector64.Create(_cards[n[0]].Owner, _cards[n[1]].Owner, _cards[n[2]].Owner, _cards[n[3]].Owner); // (3)
  var result = AdvSimd.CompareGreaterThan( // (4)
    Vector64.Create(card.Top, card.Right, card.Bottom, card.Left),
    Vector64.Create(_cards[n[0]].Bottom, _cards[n[1]].Left, _cards[n[2]].Top, _cards[n[3]].Right));

  var select = AdvSimd.And(result, AdvSimd.CompareGreaterThan(owners, Vector64<short>.Zero)); // (5)
  var selected = AdvSimd.BitwiseSelect(select, Vector64.Create(card.Owner), owners); // (6)

  for (var i = 0; i < 4; i++) // (7)
  {
    _cards[n[i]].Owner = selected.GetElement(i);
  }
}

It’s now pretty dense, so let’s break it down line by line:

1. The very first action is to place a card. Due to the way we have indexed the board, we can find the correct place by multiplying the row by 3 and adding the col.
2. Next, using the _neighbors lookup table, we get the four neighbors n.
3. Now we need to create a vector of owners of the neighbor cards. We will use it in two places.
4. But first, we also need to get the result of the value comparisons. We do that by creating two vectors: one with the card values, and the other with the adjacent values of the neighbor cards. Then we execute AdvSimd.CompareGreaterThan on them, which compares corresponding elements of the vectors and returns a new resulting vector with 0s and 0xFFFFs, indicating if the element in the first vector is greater than its correcting part in the second vector or not.
5. We do a similar operation, but for owners, applying AdvSimd.CompareGreaterThan to the owners vector and a vector of zeros. After which we immediately AND them with AdvSimd.And. So we know which neighbors should change the owner.
6. To actually change the owners, we apply AdvSimd.BitwiseSelect on the vector we got in the previous step. AdvSimd.BitwiseSelect is an interesting intrinsics that returns a new vector where each bit is chosen from either the left vector, Vector64.Create(card.Owner), or the right vector, owners, depending on the corresponding bit in select. It works bitwise, not element-wise, so if the bit in the mask is set, the result takes the bit from the left vector, otherwise, from the right. Essentially, we are asking which cards should change owners to card.Owner and which should keep their owner.
7. Finally, we go over the neighbors one by one and assign the new owner information we got in selected.

The GetAll method also becomes simpler, it just creates a span by slicing the _cards array to remove the virtual neighbors:

public ReadOnlySpan<Card> GetAll()
{
  return _cards.AsSpan(0, 9);
}

That was a long ride, but now we see that we went from doing multiple if statements to doing logic without any branching. The Add method, however, did become a bit more dense (and platform-dependent). But I hope this is a good illustration that in some cases, we can rearrange the problem so that another approach, perhaps a bit more simpler and not necessarily platform-dependent, could be applied.

In addition, the branchless approach might be a bit faster in theory, but let’s be honest, with only four elements to process, it’s barely going to matter.

You can check out the code from this post on GitHub: BranchlessTripleTriad.